- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Thinking Outside the Box -- or Maybe Just About the Box
The First Box Problem
Introduction
Being able to step back and consider the problem without many constraints allows one to see the interdependence of the cut length, positioning of cuts, and the volume of the box. However, will students recognize that if they encounter the following box problem?
A sheet of cardboard is rectangular, 14 inches long and 8.5 inches wide. If six congruent cuts (denoted in black) are to be made into the cardboard and five folds (denoted by dotted lines) made to adjoin the cuts so that the resulting piece of cardboard is to be folded to form a closeable rectangular box (see figures below). How should this be done to get a box of largest possible volume?
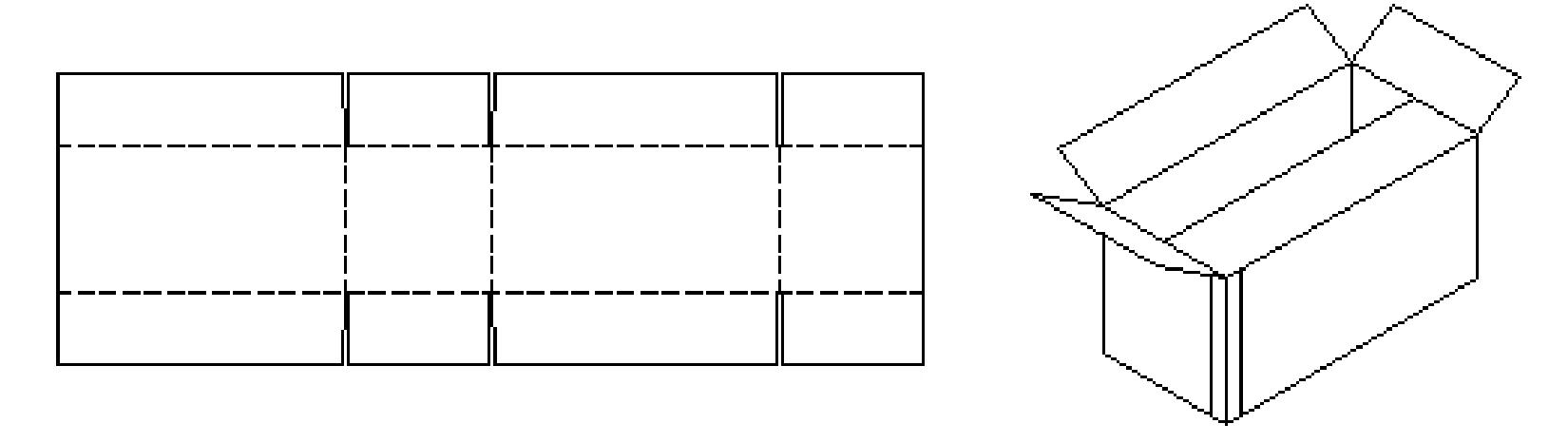
Figure 7: The box problem graphics
Before interacting with the Box Problem applet, students should be given the opportunity to physically build their own boxes out of paper or cardboard using scissors and tape or dissect a provided RSC. In doing so, students' physical constructions or destructions will help them recognize the particular physical constraints and how elements of the RSC come together prior to exploring the virtual world presented in the applets. Questions that can be asked of the students during this initial phase of exploration, if they don't naturally generate them on their own, are:
- What does a ''closeable rectangular box'' infer about the characteristics of the box?
- What impact does "closeable" have with respect to the length of at least a pair of the flaps?
- Should the flaps overlap? and
- If they do overlap, is that the best use of the cardboard?
After students have constructed boxes in this manner then we suggest that students begin to interact with a set of Java applets designed to help students interact with the problem in ways that would not be possible when building boxes out of cardboard.
But where does one go from there? Is moving expressly toward the algebraic solution the only path? It is our contention that considerably more learning can occur if this path is at least delayed a little while longer so students can be asked to explore the problem with greater depth. The pertinent question here is how does one encourage students to search for deeper insights that can be drawn from such a seemingly simple problem. We suggest the use of a pair of applets to help students investigate the problem in increasingly more complex ways and open their eyes to conditions and constraints that were not obvious through their initial encounters.
Thomas Hern (Bowling Green State Univ.) and David Meel (Bowling Green State Univ.), "Thinking Outside the Box -- or Maybe Just About the Box," Convergence (February 2010), DOI:10.4169/loci003321




