- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Kepler: The Volume of a Wine Barrel - The Wine Barrel Incident
Kepler had several children before his first wife died. In 1613, he married for the second time in a celebration in Linz, Austria. Kepler bought a barrel of wine for the wedding but questioned the method the wine merchant used to measure the volume of the barrel and thus determine the price.
In consequence, afterwards Kepler set out both to determine the correct volume of a wine barrel or cask, and to find the proportions that optimize the volume of such a barrel.
.jpg)
Figure 2. Wine barrels in the modern Spanish Pyrenees (left) and in Kepler's 1615 Nova stereometria doliorum vinariorum (p. 98, right). (Photo on left by the author; image on right used by permission of the Carnegie Mellon University Libraries.)
The drawing at right of a wine barrel lying on its side shows how the wine merchant determined the volume of the barrel, and thus the price of the wine. The merchant would insert a stick through the tap hole (at center top in the drawing) to the opposite edge of the lid of the barrel (at lower left or lower right). The length of stick that went into the barrel determined the price the merchant would charge!
To determine the volume of a wine barrel accurately, Kepler thought of the wine in a full barrel, or of any solid body, as made up of numerous thin sheets arranged in layers, and treated the volume as the sum of the volumes of these leaves. In the case of a wine barrel, each of these leaves was a cylinder (Klein, p. 209).
The animation below shows how Kepler could refine his approximation by using more and more cylinders. These cylindrical slices are taken perpendicular to the axis of the barrel. Each diameter is equal to that of the barrel at that particular height. The height of each cylinder can be made as small as we can imagine. These cylindrical slices are piled one on top of the other, with all the slices together constituting the barrel.
Figure 3. The animation illustrates how to estimate the volume of a wine barrel as a sum of volumes of cylinders. This interactive diagram also appears in the copy of this article, "Kepler: The Volume of a Wine Barrel," at MatematicasVisuales. (The applet here was re-created in Spring 2020 by Laura Turner.)
According to Otto Toeplitz (p. 83):
Working out finer approximations of various barrel shapes, [Kepler] consulted Archimedes and discovered that his own method of indivisibles had enabled him to obtain results in a far simpler and more general way than Archimedes, who had been struggling with cumbersome and difficult proofs. What he did not suspect was that Archimedes, too, had found his results by the same method of indivisibles (for the [Method] was lost until 1906!).
The reference to Archimedes' Method is to the work in which he described how he found many of his results on areas and volumes. After an old manuscript copy of this book was discovered in Constantinople in 1899, it was studied and deciphered by John Ludwig Heiberg from 1906 to 1908. The book then underwent restoration at The Walters Art Museum in Baltimore, and we can learn a lot about this fascinating work of Archimedes in the article, The Archimedes Palimpsest, in Convergence's Mathematical Treasures.
 |
Archimedes' Method for Computing Areas and Volumes Article by Gabriela R. Sanchis in Loci: Convergence in which she explains Archimedes' method based on the Law of the Lever. |
|
|
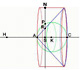
Archimedes in MatematicasVisuales - Area of a Parabolic Segment Archimedes used infinitesimal methods to discover areas and volumes 1800 years before Kepler or Cavalieri. |
Roberto Cardil (MatematicasVisuales), "Kepler: The Volume of a Wine Barrel - The Wine Barrel Incident," Convergence (January 2012), DOI:10.4169/loci003499