Geometric Photo Manipulation - Projection Formulas: Perspective

To clarify the projection methods, let's look in more detail at the example shown in Figure 3 (preceding page), in which the 400 by 400 pixel image of a storefront is pasted onto three faces of a cube in . The cube is our three-dimensional object -- its front face is the plane , and the other faces are the planes and . To project this object -- using either the perspective or the orthographic method -- we apply the color values of the pixel (counting i rows down from the top and j columns left to right in the input image) to each of three points belonging to the three visible faces of the cube. That is, letting be for the front face, for the right face, and for the top face, we apply the color of the pixel to a certain computed point of the output image.

For the perspective projection in Figure 3(a), the viewer's eye is at the point , and the viewing plane is . In this case, we find that the computed point where the line through and meets the viewing plane is

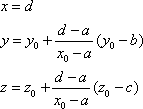
In the final step we need to identify these projected points with the pixels of an output image. One way is to begin by (roughly) estimating bounds on the calculated y and z coordinates. Let's say that all the points calculated from the scene satisfy and . Then we can use to yield appropriate row and column indices for the output image. Note that the indices are chosen so that the largest possible z value in the scene leads to the smallest row number (at the top of the image) and the smallest y value of the scene leads to the smallest column number (at the left edge of the image). The function round is applied to round to the nearest integer so that the indices of the output array are positive integers. The size of the output array can be taken to be rows and columns.

This procedure has been implemented in the MATLAB program perspective.m.