- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Logistic Growth Model - Symbolic Solutions
- Separate the variables in the logistic differential equation
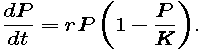
Then integrate both sides of the resulting equation. (This is easy for the "t" side -- you may want to use your helper application for the "P" side.)
- After calculating both integrals, set the results equal. If your helper application does not know about constants of integration, provide one in an appropriate place in your equation. Then solve the equation for P as a function of t.
- Now use your helper application's differential equation solver to solve the logistic equation directly. If the resulting equation is not already solved for P as a function of t, use an additional "solve" step to complete the symbolic calculation.
- The results from steps 2 and 3 are -- or should be -- formulas for the same family of functions. If the formulas do not look alike, reconcile any differences that you see. Show that one formula can be put in the form of the other. If the formulas have "arbitrary constants" in different places, show how the arbitrary constant in one formula is related to the arbitrary constant in the other formula.
- In your integration in step 2, you may have encountered ln(P) and ln(K - P), both of which make sense if P is between 0 and K. But the second one does not make sense if P > K, so your formula may not be correct in this case. Change your equation in step 2 to one that would be correct if P > K, and solve again for P. Reconcile the result with the form generated by the differential equation solver in step 3, if possible. If you think the form generated by the DE solver does not work for P > K, explain why.
- Suppose the starting population P(0) is a specific number P0 (which may be either smaller or larger than K). Choose whichever solution form you prefer, and determine the value of the "arbitrary" constant (in terms of K and P0) that produces a solution P(t) such that P(0) = P0. Simplify as much as possible.
- Explain why your solution function P(t) in step 6 approaches K as t becomes large.
- For specific values of r, K, and P0, plot the direction field and your solution function to verify visually that your formula is correct. Repeat with several combinations of the parameters, including values of P0 both smaller and larger than K.
Leonard Lipkin and David Smith, "Logistic Growth Model - Symbolic Solutions," Convergence (December 2004)




