- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Japanese Theorem for Nonconvex Polygons - A Further Generalization of Carnot's Theorem
A Further Generalization of Carnot's Theorem
When we introduced Carnot's theorem we gave a technique for computing the signed distance of a side of a polygon to the circumcenter. We must now generalize this to oriented triangles and more generally to nonconvex polygons.
Suppose we have a cyclic polygon with vertices \( p_1, \ldots, p_n . \) We now define \(d_i\), the signed distance from the \(i\)
In Figure 11 we see three different cyclic polygons with the signs of the \( d_i \) labeled. Notice that the positively oriented triangle in Figure 11(a) corresponds to the original definition.
 Figure 11
Figure 11
Carnot's theorem for oriented triangles. Let \( T \) be an oriented triangle with circumradius \( R \) and inradius \( r . \) Suppose \( a, b, \) and \( c \) are the signed distances from the circumcenter of \( T \) to the sides of \( T \) and that \( \tilde{r} \) is the signed inradius. If \( T \) is positively oriented, then \( R + r = R + \tilde{r} = a + b + c . \) If \( T \) is negatively oriented, then \( - R - r = - R + \tilde{r} = a + b + c . \)
Proof. If \( T \) is positively oriented, then this is simply the usual Carnot's theorem. Suppose \( T \) is negatively oriented. The signed distances to the sides are the negatives of what they would have been had the triangle been positively oriented. Thus, by Carnot's theorem \( R + r = - a - b - c , \) and by definition \( \tilde{r} = - r . \)∎
Generalized Carnot's theorem for cyclic polygons. Suppose \( P \) is a cyclic \( n \)-gon that is triangulated by diagonals. Let \( d_1, \ldots, d_n \) be the signed distances from the sides of \( P \) to the circumcenter and let \( d_1, \ldots, d_n \) be the signed inradii of the triangles in the triangulation. Suppose there are \( p \) triangles that are positively oriented and \( q \) that are negatively oriented. Then
\[ R ( p - q ) + \sum_{k=1}^{n-2} \tilde{r_k} = \sum_{i=1}^n d_i . \]
Proof. This is a proof by induction on the number of vertices. We may assume they are all distinct; if not, . The base case, \( n = 3 \) is simply Carnot's theorem for oriented triangles. Now suppose the theorem holds for all \( 3 \leq i \leq n \) for some \( n . \) Let \( P \) be a cyclic \( (n+1) \)-gon that is triangulated by diagonals. Furthermore, suppose it has \( p \) triangles that are positively oriented and \( q \) that are negatively oriented. By the pigeonhole principle there is a triangle that has two edges in common with \( P . \) Without loss of generality, we may assume that this triangle has vertices \( p_1, p_n \) and \( p_{n+1} , \) that the signed distances to the two edges shared with \(P\) are \(d_n , \) and \( d_{n + 1} , \) and that the signed inradius of this triangle is \( \tilde r_{n-1} . \) Remove this triangle to obtain a cyclic \( n \)-gon \( P^{\prime} . \) The key fact is that the sign of the signed distance to the newly created side (which has endpoints \( p_1 \) and \( p_n \) is different if viewed as an edge of \( P^{\prime} \) and as an edge of the triangle. (For example, in Figure 12 the sign is positive if viewed as a side of \( P^{\prime} \) and negative if viewed as a side of the triangle.) Let \( d_n^{\prime} \) be the signed distance to this side of \(P^{\prime}\) and \( -d_n^{\prime} \) be the signed distance to this side of the triangle.
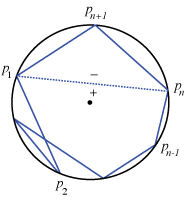 Figure 12
Figure 12
Case 1: the removed triangle is positively oriented. By the induction hypothesis
\[ \sum_{k=1}^{n-2} \tilde{r_k} = R ( q - p + 1) + d_n^{\prime} + \sum_{i=1}^{n-1} d_i . \]
Now consider the removed triangle. By Carnot's theorem for oriented triangles, \( R + \tilde{r}_{n-1} = - d_n^{\prime} + d_n + d_{n+1} . \) Consequently,
\(\sum_{k=1}^{n-1} \tilde{r_k} = \left( \sum_{k=1}^{n-2} \tilde{r_k} \right) + \tilde{r}_{n-1} \)
\( = \left( R ( q - p + 1) + d_n^{\prime} + \sum_{i=1}^{n-1} d_i \right) + ( - R + (- d_n^{\prime} + d_n + d_{n+1})) \)
\( = R(q-p) + \sum_{i=1}^{n+1} d_i , \)
as was to be shown.
Case 2: the triangle is negatively oriented. This case proceeds similarly, except that the induction hypothesis gives
\[ \sum_{k=1}^{n-2} \tilde{r_k} = R(q - 1 - p) + d_n^{\prime} + \sum_{i=1}^{n-1} d_i \]
and for the removed triangle \( - R + \tilde{r}_{n-1} = -d_n^{\prime} + d_n + d_{n+1} . \)
Case 3: the triangle is degenerate. In this case two or three of the vertices \( p_1, p_n , \) and \( p_{n+1} \) coincide. Because \( \tilde{r}_{n-1} = 0 , \) our induction hypothesis gives us
\[ \sum_{k=1}^{n-1} \tilde{r}_k = \sum_{k=1}^{n-2} \tilde{r}_k = R (q - p ) + d_n^{\prime} + \sum_{i=1}^{n-1} d_i . \]
We now consider three subcases. (a) Suppose \( p_1 = p_{n+1} . \) Then \( d_{n+1} = 0 \) and \(d_n = d_n^{\prime} . \) So \( d_n^{\prime} = d_n + d_{n+1} . \) Substituting this into the formula yields the desired conclusion. (b) The case \( p_n = p_{n+1} \) is similar. (c) Suppose \( p_1 = p_n . \) Then \( d_n^{\prime} = 0\) and \(d_n + d_{n+1} = 0 . \) Thus, the result follows.∎
David Richeson, "The Japanese Theorem for Nonconvex Polygons - A Further Generalization of Carnot's Theorem," Convergence (December 2013)




