- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
James Gregory and the Pappus-Guldin Theorem - Gregory's Proof Revealed
With all of this proportion theory in hand, Gregory's proof of the Pappus-Guldin Theorem falls into place relatively easily. Suppose that AB is the geometrical figure which is to be rotated around an axis and that a is its center of gravity. The central idea of his proof is to use the proportional version of the theorem given in the last section to compare AB with another, easy-to-understand 2-dimensional figure. In this case, that figure is a rectangle HIJK and its axis of rotation is simply the side HI of the rectangle.
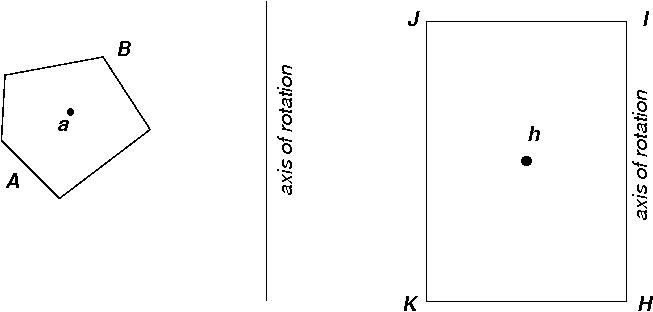
For a rectangular figure HIJK, we have area(HIJK) = HI×HK. Since the solid of revolution obtained by revolving HIJK around the the line HI is a cylinder with height HI and radius HK, we get rev(HIJK) = πHI×HK2. Finally, the center of gravity h of a rectangle is the geometrical center of the rectangle, so the distance from h to HI is (1/2) HK and thus circum(h) = 2π×(1/2)HK = πHK. With some algebraic simplification, the proportional version of the Pappus-Guldin theorem from the last section then becomes
\[\eqalign{ {rev(AB) \over \pi HI\times HK^2 } &= {area(AB) \over HI\times HK} \times { circum(a) \over \pi HK} \cr &= {area(AB) \times circum(a) \over \pi HI \times HK^2} \cr }\]
In particular, the denominators on both sides of the equation are the same. Consequently, the numerators must be equal as well. That is,
\[rev(AB) = area(AB) \times circum(a)\]
which is precisely the Pappus-Guldin theorem.
Andrew Leahy (Knox College), "James Gregory and the Pappus-Guldin Theorem - Gregory's Proof Revealed," Convergence (February 2010), DOI:10.4169/loci003262




