- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Iterative Methods for Solving Ax = b - The SOR Method
A third iterative method, called the Successive Overrelaxation (SOR) Method, is a generalization of and improvement on the Gauss-Seidel Method. Here is the idea:
For any iterative method, in finding
Here is how we derive the SOR Method from the Gauss-Seidel Method. First, notice that we can write the Gauss-Seidel equation as
so that
We can subtract
Now think of this as the Gauss-Seidel correction ![]() x
x
where, as we just found,
and where generally
Written out in detail, the SOR Method is
We can multiply both sides by matrix D and divide both sides by ω to rewrite this as
then collect the
 .
.When we solve for x(k+1), we get
Notice that the SOR Method is also of the form ![]() ,
,
so optimal convergence is achieved by choosing a value of ω that minimizes
As we did earlier for the Jacobi and Gauss-Seidel Methods, we can find the eigenvalues and eigenvectors for the
In practice, we typically use a computer to perform the iterations, so we need implementable algorithms in order to use these methods for
| Method | Algorithm for performing iteration k + 1: for i = 1 to n do: |
|---|---|
| Jacobi |  |
| Gauss- Seidel |
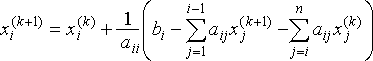 |
| SOR |  |
David M. Strong, "Iterative Methods for Solving [i]Ax[/i] = [i]b[/i] - The SOR Method," Convergence (July 2005)




