- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Math March Madness - Highlights from the 2005 Putnam Competition
Math March Madness — Highlights from the 2005 Putnam Competition
By Joseph A. Gallian
The NCAA basketball tournament is not the only manifestation of March madness. Results from the annual Putnam competition are also announced every March. The Sixty-sixth annual Putnam competition, held in December 2005, had 3545 participants from 500 institutions and 395 teams. Harvard won the team competition for the 25th time, while Princeton, which has never won the team competition, finished second for the ninth time. Duke had no one finish in the top 16 and only one in the top 24, but its team finished third for the fifth consecutive year. It was also the fifth consecutive year in which the Duke Putnam team did better than the Duke basketball team. Coincidentally, the last time Duke's team won the Putnam Competition, the announcement came in late March 2001, within a few days of Duke's basketball team winning its last national championship.
Although MIT had three of the six winners, seven of the highest 15 scorers, and 23 of the top 75, it placed only fourth in the team competition. The University of Waterloo finished in the top five for the 17th time. Alison Miller won the Elizabeth Lowell Putnam Prize as the highest finishing woman and became the first woman ever to be a member of the winning team. Three of the top five three-person teams included women. The top five scores on the 120 point exam ranged from 100 to 80. The 2005 competition is the fourteenth in which ties resulted in there being more than five winners. Twelve of these ties have occurred since 1970.
The median score was one point. This was the sixth time in the last seven years that the median score was one or zero.
Counting multiplicity, 103,812 people have taken the Putnam exam over the course of its history. In total, there have been 257 individual winners of the competition; 364 counting multiplicity. In the 2005 competition Daniel Kane of MIT was a winner for the third time in three attempts. He is the twenty-second person to win the competition three times or more. Matthew Ince of MIT was a winner while his twin brother Nathan, also from MIT, received honorable mention.
All six Putnam Fellows are former members of the U.S. Mathematics Olympiad team. Remarkably, only two seniors from the United States ranked among the top 24 scorers. Judging from the top 196 scorers, the following problem was the most difficult with only five participants receiving any points.
[B5] Let P(x1,Â…,xn) denote a polynomial with real coefficients in the variables x1, Â…, xn, and suppose that
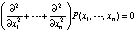 Identically
Identically
and that 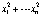 divides P(x1,...,xn)
divides P(x1,...,xn)
Show that P = 0 identically.
A comprehensive up-to-date history of the Putnam competition is available at http://www.d.umn.edu/~jgallian/putnam05.pdf.
Joe Gallian is a member of the FOCUS editorial board.
id:
4101
News Date:
Tuesday, May 23, 2006




