Beautiful Geometry

Geometry is, of course, a highly visual subject, and most if not all geometry books come with pictures of various geometric objects like circles and triangles. Some, like Barnes’ Gems of Geometry, even provide color pictures. This book, however, takes things to an entirely new level; what we have here can reasonably be described as a cross between a mathematical coffee table book and a textbook.

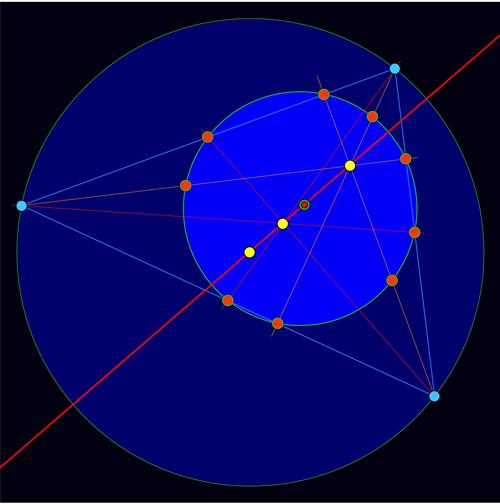Beautiful Geometry is the product of collaboration between a mathematician (Maor) who has written several other mathematics books, such as Trigonometric Delights and The Pythagorean Theorem: A 4,000 Year History, usually intended for a reasonably general audience, and an artist (Jost) with an interest in geometry. There are 51 short chapters, each containing two or three pages of text written by Maor, as well as a full-page color plate, created by Jost, illustrating the subject matter of that chapter. The written exposition contains a brief description of what the artwork demonstrates. The image to the left appears in chapter 41, “The French Connection.”

The chapters cover a wide variety of topics, assembled in roughly historical order. So the first chapter, for example, is about Thales, and subsequent chapters address a number of classical Greek results (the Pythagorean theorem gets two chapters, and a number of chapters also discuss straightedge/compass constructions, including the impossible ones of squaring the circle and doubling the cube, as well as constructions that are not impossible, such as the golden ratio and the regular 17-gon).

Proceeding further ahead in time, we encounter conics and other curves like the cycloid, epicycloid and hypocycloid; there are also several chapters on what might be described as “advanced Euclidean geometry”: Ceva’s theorem, Steiner’s porism, Morley’s theorem, the Euler line, and Pick’s theorem. In addition, the subject of symmetry (including the multiplication table of the group of symmetries of an equilateral triangle) is discussed in a pair of chapters, and two other chapters (one on the snowflake curve, the other on the Sierpinski triangle) introduce the reader to fractals.

The book’s title notwithstanding, some of the chapters seemed rather tenuously related to geometry. Several, for example, were number-theoretic in nature; two had prime numbers as their subject, and specific numbers like 11 and 50 were the subject of their own chapters as well. The number e gets a chapter, as do the Fibonacci numbers. (There is no chapter entitled \(\pi\), but this number is the star of several chapters, including one called “Archimedes Measures the Circle” and another titled “The Digit Hunters”, about attempts to approximate \(\pi\).)  

The final chapter (“Beyond Infinity”) is also not really “geometrical”; it is a brief introduction to infinite sets and cardinality. The theme of infinity is reflected in a couple of other chapters that addressed aspects of the limit process; there is a chapter, for example, on the harmonic series, and one that proves .9999… = 1.

The mathematics discussed in this book is not just purely expository and informal. To answer the perennial question of mathematics students over the years: “yes, there are proofs.” Some appear in the body of the chapters, and others appear in an Appendix. Most are quite standard (the irrationality of the square root of 2, for example) and will be familiar to most or all readers of this column, but I did see a physics-based proof of Ceva’s Theorem that was new to me. There are no exercises, however.

So much for the text; what about the pictures? Appreciation of art is obviously a matter of individual taste. The various pictures in this book are visually appealing and I enjoyed perusing them, but thought that, overall, they were more interesting than beautiful. One plate, for example, consists of the number 73939133, followed in successive rows by the number obtained by deleting the right-most digit of the number above it; it turns out that all these numbers are prime. Cute, but certainly nothing I would hang on any of the walls of my home. The chapter on squaring the circle mentions a Biblical verse which would give a value of 3 for \(\pi\) and the accompanying art depicts a large circle with the equation “\(\pi= 3\)” in the circle, and the Hebrew verse itself written around the circumference. This is again something that I thought was quite interesting but not conventionally beautiful. Yet another example like this occurs in chapter 41, with a picture of a triangle with numerous centers, associated circles and lines depicted in a mixture of colors.

Some of the art was quite striking. Chapter 44, on symmetry, for example, had a very attractive picture of circles inside of a larger circle, with the smaller circles all exhibiting various symmetry patterns. (See above.) All the artwork shows careful attention to (often intricate) detail.

All told, while I wouldn’t recommend buying this book just for the art, I thought the combination of art and exposition was quite effective. The writing is accessible to most reasonably well-educated laypeople, and I imagine that many such people would derive considerable pleasure dipping into this attractive and interesting book.

Mark Hunacek ([email protected]) teaches mathematics at Iowa State University. 

Images used with permission of Princeton University Press.