- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Kepler: The Volume of a Wine Barrel - Solving the Problem of Maxima: Wine Barrel Design
To optimize the volume of the wine barrel, Kepler simplified the problem. He approximated the barrel by a cylinder with the diagonal measurement \(d=SD,\) radius of the base \(r,\) and height of the cylinder \(h.\) In modern notation, the formula for the volume \(V\) of a cylinder is: \[V=\pi r^2h.\]
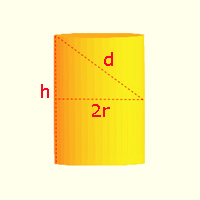
Using the Pythagorean Theorem, we can write an equation relating \(d, h,\) and \(r:\) \[d^2 = \left(\frac{h}{2}\right)^2 + (2r)^2.\]
Now solve for \(r^2:\) \[r^2 =\frac{d^2}{4}-\frac{h^2}{16}.\]
Hence, we can deduce the formula for the volume \(V\) as a function of \(h\) and \(d:\) \[V=\frac{\pi}{4}d^2h-\frac{\pi}{16}h^3.\]
For fixed \(d,\) the volume \(V\) is a function of height \(h,\) and we would like to see how the volume \(V\) changes when we modify the height \(h\) of the barrel.
Figure 7. For a fixed value of \(d,\) the volume \(V\) is a function of height \(h.\) The graph at left shows how, for a fixed value of \(d,\) changes in height \(h\) result in changes in volume \(V.\) The figure at right shows how, for a fixed value of \(d,\) changing the height \(h\) changes the radius \(r\) and the shape of the cylindrical barrel. This interactive diagram also appears in the copy of this article, "Kepler: The Volume of a Wine Barrel," at MatematicasVisuales. (The applet here was re-created in Spring 2020 by Laura Turner.)
Next, Kepler asked: "If \(d\) is fixed, what value of \(h\) gives the largest volume \(V\)?" (Toeplitz, p. 83). After making some calculations and comparing them, he decided the answer was: \[h=\frac{2d}{\sqrt{3}}.\]
According to Toeplitz (p. 83):
That defined a barrel of definite proportions. Kepler noticed that in his Rhenish homeland barrels were narrower and higher than in Austria, where their shape was peculiarly close to that having a maximum volume for a fixed \(d\) - so close, indeed, that Kepler could not believe this to be accidental. So he imagined that centuries ago somebody had calculated barrel shapes, as he himself was doing, and had taught the Austrians to construct their barrels in this particular fashion - a very practical one, indeed. Kepler showed that if a barrel did not satisfy the exact mathematical specification \[3h^2 = 4d^2,\] but deviated somewhat from it, this would have but little effect on the volume, because near its maximum a function changes only slowly.
That the volume function changes very slowly near its maximum value is illustrated in the graph below.

Figure 8. For a fixed value of \(d,\) the graph of volume \(V\) as a function of height \(h\) illustrates that, near the maximum volume, small changes in height \(h\) result in small changes in volume \(V.\)
Kepler tabulated values obtained by calculation to reinforce his idea that the volumes of such cylinders with equal diagonals change very little in the neighbourhood of a maximum (Baron, p. 116).
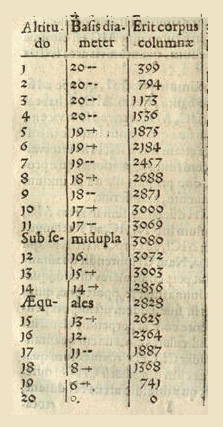
Figure 9. Kepler's table of volumes of wine barrels of various heights (altitudes) from p. 66 of his 1615 Nova stereometria. View this page and the whole book at The Posner Memorial Collection: Kepler's Nova Stereometria. (Image used by permission of the Carnegie Mellon University Libraries)
But what about the barrel of wine Kepler had purchased for his wedding in Austria? Was it priced fairly? According to Toeplitz (p. 83):
Thus, while the Austrian method of price determination, if applied to Rhenish barrels, would be a clear fraud, it was quite legitimate for Austrian barrels. The Austrian shape had the advantage of permitting such a quick and simple method. So Kepler relaxed in this instance.
This, then, was the major contribution by Kepler: He noted that as the maximum volume was approached, the change in the volume for a given change in the dimensions became smaller. Some years later, Fermat would consider maximum and minimum problems of this kind from a similar point of view.
Roberto Cardil (MatematicasVisuales), "Kepler: The Volume of a Wine Barrel - Solving the Problem of Maxima: Wine Barrel Design," Convergence (January 2012), DOI:10.4169/loci003499




