- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
The Mathematics of Levi ben Gershon in the Classroom
Editor's note: The journals of the National Council of Teachers of Mathematics (NCTM) have published numerous articles on the history of mathematics and its use in teaching. These journals include Teaching Children Mathematics, Mathematics Teaching in the Middle School, and Mathematics Teacher. Thanks to the efforts of Convergence founding co-editor Frank Swetz, NCTM allows Convergence to republish (in pdf format) two articles from Mathematics Teacher annually. One of the editor’s picks for 2017 is the article, “The Mathematics of Levi ben Gershon,” by Shai Simonson on using examples from the work of Rabbi Levi ben Gershon (1288-1344) in today's classrooms:
Shai Simonson, “The Mathematics of Levi ben Gershon,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 659-663. Reprinted with permission from Mathematics Teacher, © 2000 by the National Council of Teachers of Mathematics. All rights reserved.
(To download a pdf file of the article, “The Mathematics of Levi ben Gershon,” click on the title of the article.) Simonson recently shared additional excerpts from Levi ben Gershon's 1321 mathematical work, Maaseh Hoshev (The Art of the Calculator), and how he has used them in a college course for prospective mathematics teachers. All translations from Hebrew to English are by Simonson.
More Classroom Resources from Levi ben Gershon's Maaseh Hoshev
By Shai Simonson (Stonehill College)
Over the years, I have used a number of sections from Levi’s Maaseh Hoshev in a class I teach at Stonehill College to prospective mathematics teachers. This class, required by the state of Massachusetts for elementary and middle school math teachers, is supposed to focus on mathematical content and its relation to teaching. There is a great deal of material in Maaseh Hoshev, including theorems and proofs from Part 1 of the manuscript, arithmetic algorithms from Part 2, and of course, the two problems discussed in the NCTM Mathematics Teacher article, "The Mathematics of Levi ben Gershon." There is also an interesting biblical commentary of Levi relating to calculating \(\pi\) with body measurements, which the students find interesting and entertaining (see below).
The sections I use most often include theorems about combinations, permutations, sums of integers, squares, and cubes from Part 1 of the Maaseh Hoshev, square and cube root algorithms from Part 2 (see below), various samples of the 21 questions in the problem section, and the biblical commentary about \(\pi\) (see below). Some of these resources are included in this article.
There are many ways to use these materials creatively in the classroom, and I have no conclusive claim for the best way. Generally, I have students try to solve problems themselves, and then compare what they did to the methods written in these resources. This encourages problem solving, enables practice reading and interpreting mathematics, and asks for analysis in the comparison of methods.
Resource 1: Six More Problems from Maaseh Hoshev
The article, "The Mathematics of Levi ben Gershon," in Mathematics Teacher discusses problems 8 and 6 (in that order) of the 21 problems in Levi’s Maaseh Hoshev. Below are problems 3, 4, 5, 7, 11, and 12, which all mention the coin discussed in problem 8. In the resources below, the indented text is the translation from Hebrew of Levi's work, and the text that is not indented contains my comments.
In class, I have students working in groups try to solve these problems on their own using any methods they can devise. After the groups share their methods, we read through Levi’s methods and try to decipher exactly what he is suggesting, and why his idea works. This begins a discussion comparing Levi’s methods to the ones discovered by the student groups.
Problem 3: The cost of a given quantity of a product is given. What is the cost of a second given quantity of this product?
Multiply the given cost by the second given quantity, divide by the first given quantity and this is what was requested.
For example, the cost of 11 measures of wheat is 7 dinars, and you want to know the cost of 15 measures of wheat. Multiply 7 by 15 and divide by 11, to get 9 whole and 6 of 11 parts of one, which is what was requested. That is, the cost of 15 measures is 9 dinars and 6 of 11 parts of a dinar.
This is right, because the ratio of the first quantity to the second quantity equals the ratio of the known cost to the unknown cost. This is self-evident. Thus, the product of the second quantity with the known cost equals the product of the first quantity with the unknown cost. And use this as a model.
Here is the method to convert a given fraction of the day into hours and fractions of an hour, or to convert a given fraction of the litra, which is 20 dinars, into dinars and peshuts and fractions of a peshut, or to convert anything that is made up of a known number of parts.
For example, we want to know how many hours and fractions of an hour there are in 83 of 109 parts of a day. We know that the number of hours in a day is 24. So the ratio of 83 to 109 equals the ratio of the unknown number of hours to 24. Multiply 24 by 83, divide by 109, and that is what was requested. That is approximately 18 hours, 51 firsts and 12 seconds.
Levi uses base 10 for integer parts and base 60 for fractional parts of a number. This was very common in his time. Therefore, “firsts” and “seconds” should be interpreted appropriately here as minutes and seconds. Note however, that the answer is wrong. The correct answer is approximately 18; 16, 31. In other examples of conversion to base 60 throughout these problems, Levi gets the answers precisely correct, so one should not speculate that there is some flaw in his method, rather that the numbers were corrupted, and represent scribal errors. This is the first error of several similar errors found in all the extant manuscripts.
If the example used a litra, then since we know that the number of dinars in a litra is twenty, the ratio of 83 to 109 equals the ratio of the unknown to twenty. Multiply twenty by 83 and divide by 109, to get 15 dinars and 15 of 109 parts of a dinar. You can now find the value in peshuts by multiplying 12 by 106 and dividing by 109, to get 11 peshuts and 73 of 109 parts of a peshut, which is approximately 2 thirds of one peshut. In this way, you can handle similar things.
The passage above states explicitly that there are 20 dinars in a litra and implies that there are 12 peshuts in a dinar. A litra is a measure of weight, translated commonly as a pound, and the peshut and dinar are coins, hence there are 240 peshuts to a pound.
The peshut is almost surely the denier, a paper thin lightweight coin of mixed silver and copper, and the standard coin of Europe for 500 years between the 8th and 13th centuries. The dinar is just as surely the gros tournois, a heavy royal French silver coin introduced by King Louis IX of France in 1266, which became the standard coin of Europe from the late 13th through 14th century. The Jewish traveler Eshtori ha-Farhi mentions the use of coins in Provence in the 14th century. Farhi writes that there is a small coin that the Arabs called a pashit, twelve of which are one "white tournois". No doubt that the Arab pashit is the Hebrew peshut, and this in turn is the denier, while the white tournois is the gros tournois. There were indeed 12 deniers in a gros tournois and 240 deniers in a pound. Note the 12 crowns around the circumference of the coin in the figure shown in the article, "The Mathematics of Levi ben Gershon," in Mathematics Teacher.
The terms dinar and peshut are found in the Talmud, referring to generic large and small denominations respectively. Levi seems to use the anachronistic Talmudic names for real coins of his day. Note that what was called a dinar in his day, was the standard Muslim gold coin, worth a great deal more than Levi’s dinar. Later on, Levi will give a problem where he talks about dinars and gold dinars. Presumably, the latter is the dinar of his day, and the former is the gros tournois.
The next four paragraphs are found in all nine of the first edition manuscripts of Maaseh Hoshev. In the three second edition manuscripts, they are in the text of one (the Jerusalem manuscript), copied in the margin of another (Moscow 1063), and omitted from the third (Moscow 30).
Here is the method for converting a variety of fractions to one fraction. Take the prime denominator of the various denominators of the fractions, extract the fractions from it, and the result is the fraction of the common denominator.
For example, if you wanted to convert 3 sevenths and 4 parts of 17 to a single fraction, then take these parts from the common denominator which is 119, and the result is 79 parts of 119.
Here is the method for converting the parts of a given fraction to a unit fraction. Divide the denominator of this fraction by the numerator, and the result is what was requested.
Levi uses the previous two methods throughout the problem section.
For example, if you wanted to convert 3 sevenths to a unit fraction, divide seven by 3, to get 2 and a third. This is one of 2 and a third parts of that from which we wanted to extract 3 sevenths. And use this as a model.
“This” in the second sentence of the last paragraph refers to 3/7. The wording in Hebrew is also ambiguous.
Problem 4: A traveler on a steady journey, walks a fixed distance in a given amount of time. How far will he walk in a second given amount of time?
Multiply the second given amount of time by the fixed distance, divide the result by the given amount of time, and you will get what was requested. If one or both of the times contained hours, then convert the amount of time to hours, where hours are the whole unit.
For example, the traveler traveled 7 measures, 36 firsts and 57 seconds in 13 days, and we want to know: how far would he travel in 3 days, 17 hours, 52 firsts and 16 seconds? We convert the days to hours so that the first given time is 312 and the second time is 89 whole, 52 firsts and 16 seconds. We multiply 7 whole, 36 firsts and 57 seconds by 89 whole, 52 firsts and 16 seconds. We divide the result by 312 to get 2 whole, 10 firsts and 56 seconds. This is the number of measures that he walked in the second given amount of time.
This is an error. The correct answer is approximately 2; 11, 37. Note that the numbers 52 and 22 look alike in Hebrew, and that if 22 is used instead, then the answer is 2; 10, 53, which is much closer to the given answer but still incorrect. One of the 12 extant manuscripts of Levi's Maaseh Hoshev has 22 for the first occurrence of 52, but not for the second. It is not clear what the correct numbers should be in this example.
This is right, because in a steady journey, equal times make equal measures. Therefore, the ratio of time to time equals the ratio of journey to journey.
You can now consider the reverse problem. That is, the problem is posed given a steady journey where a given distance is walked in a given amount of time. How much time will it take to walk a second given distance? Multiply the second given distance by the given time, converting the days to hours to make it easier. Divide the result by the first given distance and this is what was requested.
For example, the traveler walks 7 measures, 36 firsts and 57 seconds in 13 days. We want to know: how much time will it take him to walk 3 measures? We multiply 3 measures by 312 whole, and divide by 7 whole, 36 firsts and 57 seconds, to get 122 hours, 54 firsts and 7 seconds, which is the unknown time. This is explained by the very same reason as before.
This answer is correct to the nearest second. Note that 54 firsts is 54 minutes.
Problem 5: If two travelers, one faster than the other, are traveling steady journeys, and the distance between the faster, who is behind, and the slower, is a fixed measure; how much time will it take the faster to catch the slower?
Divide the fixed measure, by the excess distance traveled by the faster over the slower in an hour. The result is the number of hours and fractions of an hour that it takes the faster to catch the slower.
For example, the faster travels 2 measures and 37 seconds in an hour, the slower travels 30 firsts and 24 seconds in an hour, and the distance between the slower, who is in front, and the faster, is 29 measures and 45 firsts. The excess distance traveled by the faster over the slower in an hour, is one measure, 30 firsts and 13 seconds. We divide this into the given distance to get 19 hours, 47 firsts and 9 seconds. The reason for this is clear from the previous discussion.
The result 19 hours, 47 minutes and 9 seconds is correct to the nearest 3600th but not exact. In this case, Levi usually says that the result is a close approximation, but here he does not.
Problem 7: The cost of a given item is a certain number of dinars. What is the cost of a given set of fractions of this item?
Take the common denominator of all the fractions, and extract the fractions from it. Then find the cost of this result, multiply by the number of the item, and divide by the common denominator, to get what was requested.
For example, the cost of a gold dinar is 25 dinars, and we want to know: what is the cost of a dinar with half of it, 2 sevenths of it, and 3 fourths of it? The common denominator of these fractions is 28. You extract these fractions from it to get 71. You multiply 71 by 25 to get a thousand and 775, and this is the cost of these extracted fractions. Multiply this number, by the size of the purchase which is one, and divide by 28, to get 63 whole and 11 of 28 parts of one, which is the cost. That is, 63 dinars and 11 of 28 parts of a dinar. You can check this if you wish.
Here we see that Levi distinguishes between the gold dinar which is the standard Muslim dinar, and the dinar which is the gros tournois. See the commentary in Problem 3 above.
This is right, because the ratio of the fractions extracted from the common denominator, to the fractions extracted from the gold dinar, equals the ratio of the common denominator, to one, which is the size of the item. Thus, the ratio of the cost of the fractions extracted from the common denominator, to the cost of the fractions extracted from the gold dinar, equals the ratio of the common denominator to one, because it is clear that the ratio of item to item equals the ratio of cost to cost. Hence, the product of the cost of the extracted fractions from the common denominator, with one, equals the product of the cost of the extracted fractions from the dinar, with the common denominator. And use this as a model.
The explanation is one and the same if the size of the item being sold is arbitrary. For example, the cost of 7 measures of wheat is 25 dinars, and we want to know: what is the cost of the wheat with half of it, and 2 sevenths of it, and 3 fourths of it? We extract the fractions from the common denominator which is 28, to get 71. The cost of these is 253 dinars and 4 sevenths of a dinar. Multiply this by the size of the item being sold, which is 7, divide by the common denominator, which is 28, to get 63 dinars and 11 of 28 parts of a dinar. And use this as a model.
Problem 11: A merchant sells two items at different prices, and a buyer wants to purchase a single measure of the two, for a given cost which is greater than the lower price and smaller than the higher price.
The question here is implicitly: What fraction of the measure should he buy from each item? The problem is equivalent to: Given \(a<b<c,\) \(x + y = 1,\) and \(ax + cy = b,\) find \(x\) and \(y.\)
It is appropriate to take the excess of the higher price over the lower price, and divide the measure into this many parts. Then take the deficiency of the lower price, to find the number of parts to buy from the higher priced item; and the excess of the higher price, to find the number of parts to buy from the lower priced item.
“Deficiency” and “excess” are with respect to the given cost. Levi's solution is: Let \(x = \frac{c-b}{c-a}\) and \(y =\frac{b-a}{c-a}.\)
For example, the merchant sells two drugs. The price of the first is 17 peshuts per litra, and the price of the second is 24 peshuts per litra. A buyer wants to buy a measure of the two at a cost of 19 peshuts. The excess of the higher price over the lower price is 7, so divide the measure into 7 parts. The difference between the lower price and 19 is two, so this is the number of parts of the measure that should be bought from the higher priced item. The excess of the higher price is five, so this is the number of parts that should be bought from the lower priced item. The cost of the measure is 19 peshuts. And use this as a model.
This is right, because here we have three different numbers: 17, 19 and 24. The product of 24 with two, which is the excess of the middle over the small, plus the product of 17 with five, which is the excess of the large over the middle, counts 19, the middle, as many times as the excess of the large over the small, which is 7.
Levi is implicitly referring to Theorem 45 in Part 1 of Maaseh Hoshev which states that given \(a < b < c,\) then \(c(b-a)+a(c-b) = b(c-a).\)
Hence, the sum of the cost of two litras at the price of 24 peshuts each, plus the cost of five litras at the price of 17 peshuts each, equals 7 times 19. The number of litras here is 7, hence each one sells for 19 peshuts. Furthermore, the ratio of two sevenths of a litra, to two litras, equals the ratio of five sevenths of a litra, to five litras. Accordingly, the ratio of the cost of two sevenths of a litra at the higher price, to the cost of two litras at the higher price, equals the ratio of the cost of five sevenths of a litra at the lower price, to the cost of five litras at the lower price. Accordingly, the ratio of the cost of two sevenths of a litra at the higher price plus five sevenths of a litra at the lower price, to the cost of two litras at the higher price plus five litras at the lower price, equals the ratio of the cost of two sevenths of a litra at the higher price, to the cost of two litras at the higher price.
Levi is using the well-known theorem that if \(\frac{a}{b}=\frac{c}{d},\) then \(\frac{a+c}{b+d}\) is also equal to them. He discusses this theorem and similar ones in Section (f) of Part 2.
However, the ratio of the cost of two sevenths of a litra at the higher price, to the cost of two litras at the higher price, is a seventh of the cost. Hence, the ratio of the cost of two sevenths of a litra at the higher price plus five sevenths of a litra at the lower price, to the cost of two litras at the higher price plus five litras at the lower price, is a seventh of the cost. It was already made clear that the total cost is 7 times 19. Hence, the cost of this litra is a seventh of 7 times 19, which is 19 peshuts. And use this as a model.
When Levi says that the ratio is “a seventh of the cost,” he means that the former cost is 1/7 the latter cost. That is, the ratio itself is equal to 1/7. Also, notice that Levi uses “litra” here instead of the more general “measure” used in the statement of the problem.
Problem 12: A merchant sells a number of items with different prices. A buyer comes to purchase a single measure from them all, whose total cost exceeds the lowest price and is exceeded by the higher price. What parts of the measure should he buy from each item?
This is a generalization of the previous problem from two variables to n. Levi knows that his solution is not unique, and he implies this by his comment in the next paragraph “so that the answer will be as small as possible”. He also implies that any solution must include a positive measure of each item. That is, no item can be left out.
It is appropriate to pair up each one of the lower prices with one of the higher prices. If the higher prices do not suffice with respect to the lower, since the number of higher prices is either greater or smaller, then match up each of the corresponding remaining prices, with the item whose price is closest to the desired cost, so that the answer will be as small as possible. After you complete this procedure as described for all the pairs, then sum up all the excesses of the larger number over the smaller number in each pair, and divide the litra into this many parts. If there was an item whose price is equal to the desired cost, so that this item has no pair, then take one part or many parts from this item, accordingly as you wish. Add this number of parts to the sum, and divide the litra into that many parts.
For example, the merchant sells seven drugs. The price of the first drug is 3 peshuts per litra; the price of the second drug is 5 peshuts; the price of the third drug is 8 peshuts; the price of the fourth is 11 peshuts; the price of the fifth is 15 peshuts; the price of the sixth is 19 peshuts; and the price of the seventh is 28 peshuts. A buyer wants to purchase a litra from all with 15 peshuts. There are two higher prices: the drug that costs 19 peshuts per litra, and the drug that costs 28 peshuts per litra; and there are four lower prices: the drug that costs 4 peshuts, the one that costs 5 peshuts, the one that costs 8 peshuts, and the one that costs 11 peshuts. We place 3 peshuts corresponding to 19 peshuts, and 5 peshuts corresponding to 28 peshuts. Since there are leftover drugs with lower prices but none with higher prices, we take the higher price that is closest to the desired cost 15, and this is 19. We pair up 19 with each of the remaining lower prices, as you can see in this figure.
| 3 | 5 | 8 | 11 |
| 19 | 28 | 19 | 19 |
We already know how to take a litra from each of these pairs, whose cost is 15 peshuts. Accordingly, take 4 of 16 parts of a litra from drug 3, and 12 of 16 parts of a litra from drug 19. Also, take 13 of 23 parts of a litra from drug 5, and 10 of 23 parts of a litra from drug 28. Furthermore, take 4 of 11 parts of a litra from drug 8, and 7 of 11 parts of a litra from drug 19. Also, take 4 of 8 parts of a litra from drug 11, and 4 parts of 8 from drug 19. The number of all these parts is 58, so we add two parts for drug 15, that has no pair. We divide the litra up into the resulting number of parts which is 60. We take 4 parts from drug 3, 13 parts from drug 5, 4 parts from drug 8, 4 parts from drug 11, two parts from drug 15, 23 parts from drug 19, and 10 parts from drug 28. The cost of the litra is 15 peshuts, and this is what was requested.
This is right, because it is clear from what preceded, that the cost of 4 litras at price 3, plus 12 litras at price 19, equals 16 times 15. The matter is similar for each pair of corresponding numbers. Furthermore, it is obvious that the cost of 2 litras at price 15 is equal to 2 times 15. By adding everything together, the cost of all these litras, each of which is a multiple of 15, equals 60 times 15.
However, the ratio of one of 60 parts of a litra, to a litra, equals the ratio of the price of one of 60 parts of a litra, to the price of a litra. It is clear by our previous explanation, that the ratio of the price of the sum of all the parts, to the price of the sum of the litras, which is 60 times 15, equals the ratio of one to 60. Thus, the price of the parts all together is 15 peshuts, which is one of 60 parts, of 60 times 15. And use this as a model.
Resource 2: Levi’s Method for Square Root Extraction
In class, we first discuss the relatively straightforward Babylonian method for calculating the square root of an integer to any desired accuracy. This algorithm takes an integer \(N,\) and makes a guess \(G\) at the square root. This guess is improved, with \(G\) being replaced by \[\frac{G+\frac{N}{G}}{2}.\] We then read Levi’s algorithm and try to compare his algorithm to the Babylonian algorithm.
Levi’s idea is not new. Some older readers may recognize it as the method taught to them in school. It is seen in geometric form in Chinese sources that predate him by a few centuries. Indeed, it is natural to think of the algorithm geometrically, but Levi does not. He provides no figures, or references to any relevant geometric notion. It is noteworthy that his focus is simply on the algebraic identity \((a+b)^2 = a^2 + b^2 + 2ab.\)
Levi’s method for extracting square roots of perfect squares from Part 2, Section (e), of Maaseh Hoshev is shown below. An explanation of the algorithm in plain English appears afterward with some hints and analysis to help the reader unravel Levi’s style. Be forewarned that Levi’s writing is difficult. He makes no use of equations, and very little symbolic notation. Even the simplest relationships and theorems are stated in longwinded prose.
In order to extract the square root of a perfect square, write the number in a row according to its levels, and examine the last level to see whether it is odd. If it isn’t odd, then bring down the digit from the level before it, so that the last digit is from an odd level.
Afterward, find the square closest to this number, but still smaller than it, and write the root of this square down in the root row, beneath the previous row, in the middle level between the first and last levels. And this is what we call the “result” row. And the square of this root is subtracted from the top row, and what remains is divided by twice the root. But be careful that after the division, there still remains an amount about as big as the square of the root that resulted from the division. Then write this result in the root row, in the level whose distance from the level that you divided is equal to the distance from that level to the first level.
Now take this result and multiply it by twice the root that exists, and by itself. This result is subtracted from the top row. And so you should do, until there is not one thing left in the top row.
For example, if you wished to find the square root of 82646281, since the last level is the eighth, bring down the one before it to give 82. And 81 is the square closest to this, and its root is 9. Write 9 down in the root row in the fourth level which is half way between the seventh and the first. And the square of 9 in the fourth, is 81 in the seventh. Subtract this from 82, and 1 in the seventh is left over. And this cannot be divided by twice 9, which is the current root, so bring down the one before it to give 16, and still we cannot divide by twice 9, so bring down the one before it to get 164. Divide this by twice the current root, which is 18, and the result is 9 which is the resulting root. And write this in the root row in the fourth level after the level of 164. Multiply it by twice the current root and itself, and subtract the result from the top row, and 18181 is left. Divide this by twice the current root, which on the previous side is 18 and 2 tenths, and the result is approximately 1 in the first level. And we write this in the root row in the first level. Multiply by twice the current root and itself, and subtract the result from the top row, and there is nothing left in the top row. And so, the square root of the given number is 9 thousand and 91, and that is what was requested.
And if you wish, you can check this by multiplying the root row by itself and getting the top row. And this works because of what I have already explained, that when one number is added to another, the square of their sum is equal to the squares of the two numbers and twice the product of one with the other.
| 1 | 8 | 1 | 8 | 1 | ||||
| 1 | 6 | 4 | 6 | 2 | 8 | 1 | ||
| 8 | 2 | 6 | 4 | 6 | 2 | 8 | 1 | |
| 9 | 0 | 9 | 1 |
For those readers trying to untangle Levi’s presentation, there are a few things to note:
- Levi is not completely consistent with his reference to the “top row”, nor does his example show a situation, where one must “be careful that after the division, there still remains an amount about as big as the square of the root that resulted from the division”, but there is still enough detail here, to extract the algorithm.
- When Levi speaks of writing a digit in a particular “level”, he is referring to the column for that number. For example, 6 in the 4th level is his way of saying 6000.
An Explanation of Levi’s Method
Levi’s idea is to construct the square root one digit at a time, always making sure that the square of the current approximation remains less than the original number \(N.\) If the current approximation is \(a,\) then we need to account for \(N-a^2\) by adding an appropriate \(b\) to the approximation. To this end, he reminds us that \((a+b)^2 = a^2 + b^2 + 2ab,\) hence adding \(b\) accounts for \(2ab+b^2\) of the required \(N-a^2.\) Given \(N\) and \(a,\) Levi computes \(b\) by dividing \(N-a^2\) by \(2a.\) This gives a good guess, since \(2ab+b^2\approx 2ab,\) when \(b\) is small in comparison to \(a.\)
Here is an example in Levi's style. Let’s try 3224990521. Here the last level is the tenth level, so we look at 32 rather than 3. The largest square smaller than 32 is 25, and its root is 5, so we write 5 in the middle column (under the second 9), i.e. 50,000. Then subtract 25 from 32 and you get 7 which is not divisible by 2\(\cdot\)5, so we look at 72, which is divisible by 2\(\cdot\)5, and the result is about 7 in the fourth column, i.e. 7000. So we take 7 and multiply by 2\(\cdot\)50 + 7, giving us 749 which is bigger than 724.
Whoops! We forgot that one must “be careful that after the division, there still remains an amount about as big as the square of the root that resulted from the division.” In this case, the square of the root is 49 and there is only 724–700 = 24 remaining after the division. So we take 6 and multiply by 2\(\cdot\)50 + 6. This gives 636 which we can subtract from 724 giving 88. So our current root is 56,000. Now bring down another digit and divide 889 by 2\(\cdot\)56, and we get approximately 7 in the third column (i.e. 700), which we multiply by 2\(\cdot\)560 + 7 to get 7889, which we subtract from 8899 to get 1010. The current root now is 56,700. Bring down another digit giving 10100, so that we can divide by 2\(\cdot\)567, and we get approximately 8 in the second column (i.e. 80). Multiply 8 by 2\(\cdot\)5670 + 8 to get 90,784. Note that the 10100 is the prefix of 10,100,521, while 90,784 is the prefix of 9,078,400. So, we subtract 90784 from 101005 to get 10221.
The current root is now 56,780. Then bring down another digit to get 102212 so that we can divide by 2\(\cdot\)5678, and we get approximately 9 in the first column (i.e. 9). Then multiply 9 by 2\(\cdot\)56780+9 to get 1022121, and we subtract this from 1022121 which leaves us with nothing in the top row. So, our final answer is 56789.
Levi’s Algorithm to Calculate the Square Root of a Perfect Square
The following modern presentation of Levi’s method is easier to follow but is not faithful to Levi’s style or language.
- Pair up the numbers from right to left, and count the pairs. This leaves either a pair of digits at the left end or a single digit. Let \(P\) be the number of pairs, not counting the last digit or last pair of digits, and let \(M\) be the (one or two digit) number which remains on the left end. (For example, given \(2415732,\) \(P = 3\) and \(M = 2\); given \(2389397496,\) \(P = 4\) and \(M = 23\).)
- Find the largest perfect square smaller than \(M, \) and let its square root followed by \(P\) \(0\)’s be the first approximation. Let \(A\) be this approximation.
- Let \(R = N – A^2.\)
- Divide \(R\) by \(2A,\) and let \(B\) be the result excluding all but the most significant digit. (Be very careful though, that \(2AB + B^2 \) is not larger than \(R.\) If so, then subtract one from the most significant digit of \(B\) and try again).
- Let \(R = R – (2AB + B^2) \). Let \(A = A + B\).
- If \(R = 0,\) then the answer is \(A\) and we are done; otherwise go back to step 4.
Here is a final example. Let N = 16384.
- P = 2 and M = 1.
- A = 100.
- R = 16384 – 10000 = 6384.
- B = 6384/200 \(\approx\) 30, but 2(100)(30) + (30)(30) is larger than 6384, so B = 20.
- R = 6384 – 2(100)(20) + (20)(20) = 1984 and A = 100 + 20 = 120.
- R is not 0 so go back to step 4.
- B = 1984/240 \(\approx\) 8, so B = 8.
- R = 1984 – 2(120)(8) + (8)(8) = 0, and A = 120 + 8 = 128.
- R = 0 so the answer is 128.
In class, we often discover an interesting way to compare Levi’s algorithm to the Babylonian algorithm. Hints: Notice that the value \[\frac{G+\frac{N}{G}}{2}\] that replaces \(G\) in the Babylonian algorithm equals \[G+\frac{N-G^2}{2G}.\] A careful study of Levi’s algorithm reveals that each new digit of \(G\) adds \(\}\)\(\frac{N-G^2}{2G}\)\(\{,\) where the symbols \(\}\) and \(\{\) mean that the enclosed division excludes all but the most significant digit, and that this digit is occasionally decreased when necessary, as described in step 4 of Levi’s algorithm.
Resource 3: Levi’s Commentary on the Sea of Solomon, and the Calculation of Pi
There is a well-known passage in the Bible that seems to imply that the value of \(\pi,\) the ratio of the circumference of a circle to its diameter, is precisely three. The passage describes a sea in which the priests would wash themselves. This sea is more like a great bathtub inside the Temple in which the priests could purify themselves before performing ritual functions.
(Kings I - 7:23) And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and its height was five cubits: and a line of thirty cubits did compass it round about.
This certainly seems to imply that \(\pi\) is simply \(30/10 = 3.\) Yet the ancient Egyptians and Babylonians knew better than this. Their values for \(\pi\) were \(4(8/9)^2 = 3.16049\dots\) and \(3 + 1/8 = 3.125,\) respectively. The Rabbis writing in the Talmud (300-600 C.E.), in their discussion of this passage, noted that this Biblical value of \(3\) is “by way of approximation.”
Levi ben Gershon, the faithful rationalist and biblical scholar, inspired by the Talmudic discussion in Tractate Eruvin (p. 14), writes:
And where it is said that a line of thirty cubits surround it about, is by way of approximation. Because the circumference of a circle adds about 1/7 to three measures of the diameter, a close approximation.
Levi asserts that the original biblical quote is taken out of context, and that the whole matter can be explained quite logically. He points out that the sea had a thick wall, and the diameter was measured from the edges of the outside of the walls, while the circumference was measured around the inner walls. Indeed, if we look just three verses ahead, we find:
(Kings I - 7:26) And it was a hand breadth thick, and the brim thereof was wrought like the brim of a cup with flowers of lilies: it contained two thousand baths.
Levi comments:
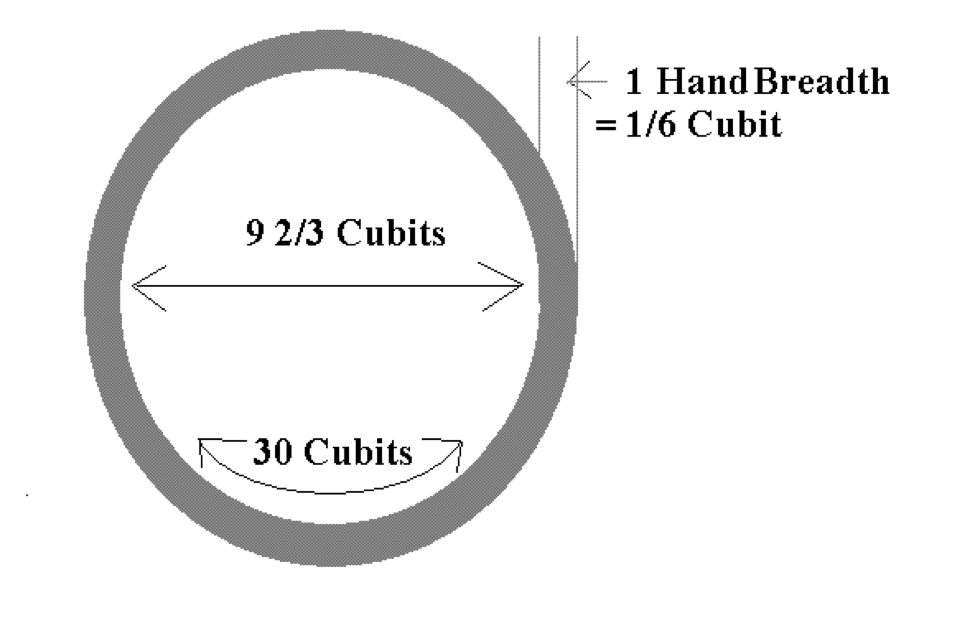
And if we say that the measurement around was taken on the inside of the basin, then that would be closer to the truth, but still just a close approximation. Since the width is a hand breadth, the diameter of the inner edge of the basin is ten cubits less one third of a cubit. And its circumference will be approximately one and one third cubits more than thirty cubits.
A cubit is the distance from the elbow to the end of the middle finger, and a hand breadth is the distance across the widest part of the hand. Ostensibly this ratio depends on each particular individual. However, for purposes of legal measurements, the Talmud, after a brief debate, establishes the ratio of cubit to hand breadth, as 1:6. A careful look at Levi’s argument shows, not surprisingly, that he too uses this ratio. And, with this 1:6 ratio, Levi derives that \(\pi\) is equal to \[\frac{30}{10-{\frac{1}{3}}}=\frac{90}{29},\] which is approximately \(3.1034\) (see Figure 1 below). This is indeed in his own words “closer to the truth but still just a close approximation.” In general, Levi’s idea yields that \(\pi\) equals \[\frac{30C}{10C-2H},\] where \(C\) is the length of a cubit and \(H\) is the length of a hand breadth.
Figure 1. Looking down into the sea: With \(H=C/6,\) \[\pi=\frac{30C}{10C-2H}.\]
A Personal Measurement of Pi Based on Your Body
If we do not use the standard Talmudic ratio of 1:6, but instead measure our own handbreadth and arm length, we can calculate a personal approximation for \(\pi\) based on Levi’s interpretation and one’s own body measurements. For example, my own cubit is 45 cm and my handbreadth is 9.2 cm. This implies that my personal approximation for \(\pi\) is \[\frac{30\cdot{45}}{10\cdot{45}-2\cdot{9.2}}=\frac{1350}{431.6}\approx{3.128}.\] When I let my students try this, some like to relate the accuracy of their approximation for \(\pi\) to the perfection of their body dimensions, but clearly Levi intended to use the 1:6 ratio and would not likely approve of this irrational amusement.
In class, each student measures another student’s cubit length \(C\) and handbreadth \(H,\) and calculates \[\frac{30C}{10C-2H}.\] We list all the values and crown a Pi King or Queen with the value closest to \(\pi.\)
Figure 2. A recent Pi King celebrates his coronation.

Did Levi Know that Pi is Irrational?
Whether or not Levi suspected that \(\pi\) is an irrational number, a number that cannot be written as a fraction \(a/b,\) makes for an interesting discussion. Levi would never make a mathematical claim without a rigorous proof to back it up, and he certainly does not make any explicit claim that \(\pi\) is an irrational number. This is not surprising considering that the first proof that \(\pi\) is an irrational number was by Johann Lambert (1728-1777) in 1767, more than 400 years after Levi lived. On the other hand, Levi was certainly aware of the proof of Hippasus (born circa 500 BCE) that \(\sqrt{2}\) is irrational, and Levi’s repeated use of the phrase “a close approximation” makes one suspect that he believed \(\pi\) is also irrational but that he had no proof. Any intelligent argument or speculation on this point needs to be based on what we know historically about mathematical knowledge in Levi’s time, and on his particular use of language. There is of course no definitive answer.
Download the NCTM Mathematics Teacher article, "The Mathematics of Levi ben Gershon," by Shai Simonson.
About NCTM
The National Council of Teachers of Mathematics (NCTM) is the public voice of mathematics education, supporting teachers to ensure equitable mathematics learning of the highest quality for all students through vision, leadership, professional development, and research. It publishes five journals, one for every grade band, as well as one on the latest research and another for teacher educators. With 80,000 members and more than 200 Affiliates, NCTM is the world’s largest organization dedicated to improving mathematics education in prekindergarten through grade 12. For more information on NCTM membership, visit http://www.nctm.org/membership.
Other Mathematics Teacher Articles in Convergence
Patricia R. Allaire and Robert E. Bradley, “Geometric Approaches to Quadratic Equations from Other Times and Places,” Mathematics Teacher, Vol. 94, No. 4 (April 2001), pp. 308–313, 319.
David M. Bressoud, "Historical Reflections on Teaching Trigonometry," Mathematics Teacher, Vol. 104, No. 2 (September 2010), pp. 106–112, plus three supplementary sections, "Hipparchus," "Euclid," and "Ptolemy."
Richard M. Davitt, “The Evolutionary Character of Mathematics,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 692–694.
Keith Devlin, "The Pascal-Fermat Correspondence: How Mathematics Is Really Done," Mathematics Teacher, Vol. 103, No. 8 (April 2010), pp. 578–582.
Jennifer Horn, Amy Zamierowski, and Rita Barger, “Correspondence from Mathematicians," Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 688–691.
Po-Hung Liu, “Do Teachers Need to Incorporate the History of Mathematics in Their Teaching?,” Mathematics Teacher, Vol. 96, No. 6 (September 2003), pp. 416–421.
Seán P. Madden, Jocelyne M. Comstock, and James P. Downing, “Poles, Parking Lots, & Mount Piton: Classroom Activities that Combine Astronomy, History, and Mathematics,” Mathematics Teacher, Vol. 100, No. 2 (September 2006), pp. 94–99.
Peter N. Oliver, “Pierre Varignon and the Parallelogram Theorem,” Mathematics Teacher, Vol. 94, No. 4 (April 2001), pp. 316–319.
Peter N. Oliver, “Consequences of the Varignon Parallelogram Theorem,” Mathematics Teacher, Vol. 94, No. 5 (May 2001), pp. 406–408.
Robert Reys and Barbara Reys, “The High School Mathematics Curriculum—What Can We Learn from History?”, Mathematics Teacher, Vol. 105, No. 1 (August 2011), pp. 9–11.
Rheta N. Rubenstein and Randy K. Schwartz, “Word Histories: Melding Mathematics and Meanings,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 664–669.
Frank Swetz, “Seeking Relevance? Try the History of Mathematics,” Mathematics Teacher, Vol. 77, No. 1 (January 1984), pp. 54–62, 47.
Frank Swetz, “The ‘Piling Up of Squares’ in Ancient China,” Mathematics Teacher, Vol. 73, No. 1 (January 1977), pp. 72–79.
Patricia S. Wilson and Jennifer B. Chauvot, “Who? How? What? A Strategy for Using History to Teach Mathematics,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 642–645.
Shai Simonson (Stonehill College), "The Mathematics of Levi ben Gershon in the Classroom," Convergence (September 2017), DOI:10.4169/convergence20170717




