- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
A Pair of Articles on the Parallelogram Theorem of Pierre Varignon

Pierre Varignon
(Source: Convergence Portrait Gallery)
Over the years, the journals of the National Council of Teachers of Mathematics (NCTM) have published numerous articles on the history of mathematics and its use in teaching. These journals include Teaching Children Mathematics, Mathematics Teaching in the Middle School, and Mathematics Teacher. Convergence founding co-editor Frank Swetz has arranged with NCTM to republish in Convergence (in pdf format) two articles from Mathematics Teacher annually. His picks for 2014 are two articles on the life and Parallelogram Theorem of French mathematician Pierre Varignon (1654-1722), including ideas for how the Parallelogram Theorem can be explored and extended in the classroom.
- Pierre Varignon and the Parallelogram Theorem, by Peter N. Oliver. Mathematics Teacher, Vol. 94, No. 4 (April 2001), pp. 316-319. Reprinted with permission from Mathematics Teacher, © 2001 by the National Council of Teachers of Mathematics. All rights reserved.
- Consequences of the Varignon Parallelogram Theorem, by Peter N. Oliver. Mathematics Teacher, Vol. 94, No. 5 (May 2001), pp. 406-408. Reprinted with permission from Mathematics Teacher, © 2001 by the National Council of Teachers of Mathematics. All rights reserved.
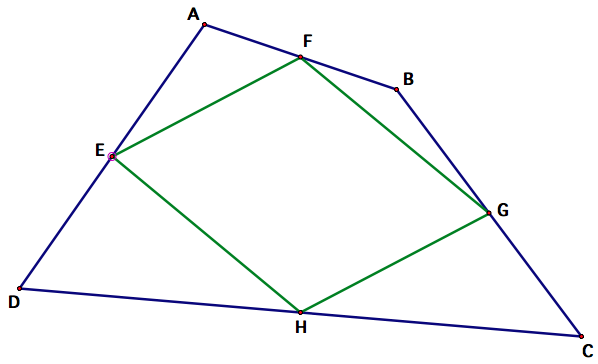
Parallelogram EFGH is formed by connecting the midpoints of the sides of quadrilateral ABCD. Is the quadrilateral formed by connecting midpoints of successive sides of any quadrilateral in fact a parallelogram?
In the second of his two articles, author Peter N. Oliver encouraged teachers to allow students to discover Varignon's Parallelogram Theorem for themselves. In 2014, he reiterated his advice, writing (via email from Honolulu, Hawaii):
Discovering the parallelogram for themselves could be a wonderful exploratory activity for second-semester geometry students. [It] would be an ideal activity for small groups of students. ... [H]ere we have a geometric investigation that is highly motivating: teachers may anticipate lively discussion as the students convince themselves that the interior figure is indeed a parallelogram, articulate a theorem, devise their proof and compose their group report. I think teachers will welcome the opportunity for students to engage in the precision of mathematical discourse.
About NCTM
The National Council of Teachers of Mathematics (NCTM) is the public voice of mathematics education, supporting teachers to ensure equitable mathematics learning of the highest quality for all students through vision, leadership, professional development, and research. It publishes five journals, one for every grade band, as well as one on the latest research and another for teacher educators. With 80,000 members and more than 200 Affiliates, NCTM is the world’s largest organization dedicated to improving mathematics education in prekindergarten through grade 12. For more information on NCTM membership, visit http://www.nctm.org/membership.
One more recommendation:
On the last page of the first of the two articles, you will see the end of another article with the intriguing title, “Geometric Approaches to Quadratic Equations from Other Times and Places,” written by Patricia R. Allaire and Robert E. Bradley. This is another of our all-time favorite Mathematics Teacher articles, which we have since reprinted as well. Be sure to take a look, using the link below.
Other NCTM Mathematics Teacher Articles in Convergence:
Patricia R. Allaire and Robert E. Bradley, “Geometric Approaches to Quadratic Equations from Other Times and Places,” Mathematics Teacher, Vol. 94, No. 4 (April 2001), pp. 308–313, 319.
David M. Bressoud, "Historical Reflections on Teaching Trigonometry," Mathematics Teacher, Vol. 104, No. 2 (September 2010), pp. 106–112, plus three supplementary sections, "Hipparchus," "Euclid," and "Ptolemy."
Richard M. Davitt, “The Evolutionary Character of Mathematics,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 692–694.
Keith Devlin, "The Pascal-Fermat Correspondence: How Mathematics Is Really Done," Mathematics Teacher, Vol. 103, No. 8 (April 2010), pp. 578–582.
Jennifer Horn, Amy Zamierowski, and Rita Barger, “Correspondence from Mathematicians," Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 688–691.
Po-Hung Liu, “Do Teachers Need to Incorporate the History of Mathematics in Their Teaching?,” Mathematics Teacher, Vol. 96, No. 6 (September 2003), pp. 416–421.
Seán P. Madden, Jocelyne M. Comstock, and James P. Downing, “Poles, Parking Lots, & Mount Piton: Classroom Activities that Combine Astronomy, History, and Mathematics,” Mathematics Teacher, Vol. 100, No. 2 (September 2006), pp. 94–99.
Robert Reys and Barbara Reys, “The High School Mathematics Curriculum—What Can We Learn from History?”, Mathematics Teacher, Vol. 105, No. 1 (August 2011), pp. 9–11.
Rheta N. Rubenstein and Randy K. Schwartz, “Word Histories: Melding Mathematics and Meanings,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 664–669.
Shai Simonson, “The Mathematics of Levi ben Gershon,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 659–663.
Frank Swetz, “Seeking Relevance? Try the History of Mathematics,” Mathematics Teacher, Vol. 77, No. 1 (January 1984), pp. 54–62, 47.
Frank Swetz, “The ‘Piling Up of Squares’ in Ancient China,” Mathematics Teacher, Vol. 73, No. 1 (January 1977), pp. 72–79.
Patricia S. Wilson and Jennifer B. Chauvot, “Who? How? What? A Strategy for Using History to Teach Mathematics,” Mathematics Teacher, Vol. 93, No. 8 (November 2000), pp. 642–645.
Peter N. Oliver (Maine Central Institute), "A Pair of Articles on the Parallelogram Theorem of Pierre Varignon," Convergence (December 2019), DOI:10.4169/Convergence20140728