- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
James Gregory and the Pappus-Guldin Theorem - A Ratio Between the Trunk and the Cylinder
For most mathematicians, the ratio that Gregory establishes between the trunk and the solid of revolution is easier to grasp than the ratio he establishes between the trunk and the cylinder. This stems largely from differences in mathematical upbringing. As noted previously, centers of gravity were an important and familiar part of the mathematical culture during the sixteenth and seventeenth centuries. But apart from the intuitive definition of the center of gravity as the balancing point for a region, they are largely absent from the training of most mathematicians today. However, the most important result for an intuitive understanding of centers of gravity is probably familiar to those who have seen second semester calculus:
Suppose "two masses m1 and m2 are attached to a rod of negligible mass on opposite sides of a fulcrum and at distances d1 and d2 from the fulcrum. The rod will balance if m1d1 = m2d2" [12, p. 554]. This is a restatement of something first given as Proposition I.6 of Archimedes' On the Equilibrium of Planes. After some division, it states the result (more amenable to someone versed in proportion theory) that two volumes balance at a point such that the ratio of the distances of this point to the centers of gravity of the volumes is reciprocally proportional to the ratios of the two volumes. That is, m1/m2 = d2 / d1. In what follows we will occasionally have need to rely on this and other intuitive results on centers of gravity.
Gregory's first task is to locate the center of gravity of the trunk. To start things off, Gregory limits himself to right cylinders constructed from figures that are symmetric about an axis perpendicular to the axis of rotation of the solid of revolution.
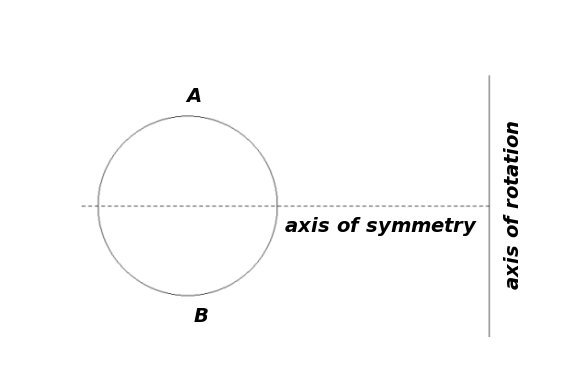
This restriction is very useful: If a figure AB is symmetric, its center of gravity will lie somewhere on its axis of symmetry. Furthermore, if a is the center of gravity of AB and b is the center of gravity of the top of the right cylindrical figure built on AB, then the center of gravity of this entire cylindrical figure lies at the midpoint X of the segment ab.
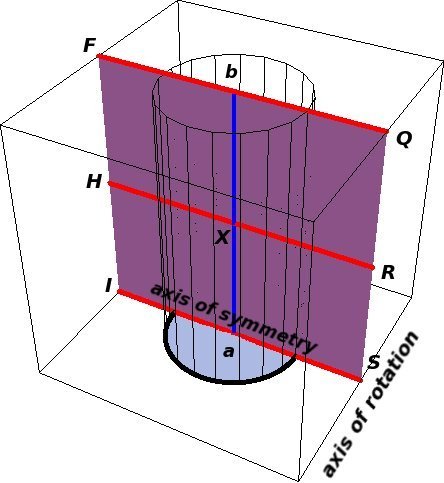
In particular, let IFQS be a rectangle which (1) passes through the axis of symmetry IS, (2) is perpendicular to the axis of rotation, and (3) has the same height FI = SQ as the cylindrical figure. Furthermore, suppose R and H are the respective midpoints of QS and FI. Then the center of gravity X of the cylindrical figure will lie at the intersection of the line segments ab and RH.
All of this can be used to determine the center of gravity of the trunk. Suppose that the (symmetrical) cylindrical figure is sliced by a plane through the axis of rotation to form an upper trunk and a lower trunk as before. For simplicity of notation, assume that the axis of symmetry IS is also a radius of rotation. Reasoning by symmetry again shows that the centers of gravity of both the upper trunk and the lower trunk will lie on the plane IFQS.
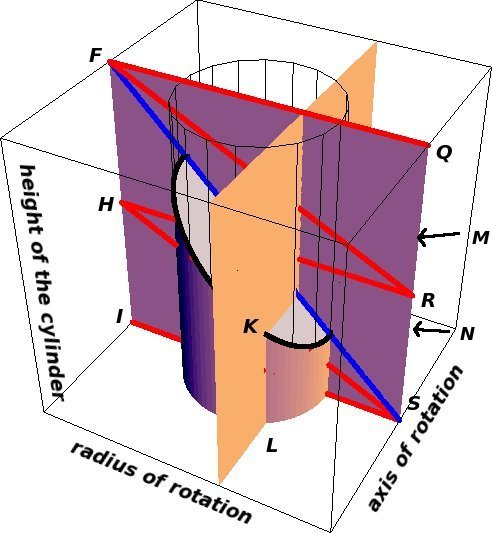
Since FI is twice HI, symmetry and Euclid VI.2 together show (with some work) that if the lower trunk is sliced by a plane perpendicular to IFQS to form a rectangular slice KLMN of the trunk, then KLMN will have its geometrical center on the line HS.
Since the geometrical center of a rectangle is also its center of gravity, it follows that the center of gravity of such a slice of the trunk will lie on the line HS. Since this is true for each slice KLMN of the trunk an argument from indivisibles then shows that the center of gravity Y of the lower trunk must lie on the line HS. A similar argument shows that the center of gravity Z of the upper trunk must lie on the line FR.
But where on HS will the lower trunk's center of gravity lie? As Archimedes had demonstrated, if the mass of the upper trunk is concentrated at its center of gravity Z and the mass of the lower trunk is concentrated at its center of gravity Y, then the center of gravity of the upper and lower trunk combined will be a point on the segment YZ such that the ratio of the distance from this point to Y and Z, respectively, will be inversely proportional to the ratio of the volume of the upper trunk to the lower trunk. But the two trunks combined make up the entire cylinder, the center of gravity of which is X.
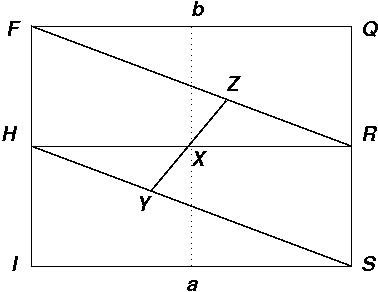
It follows that X, Y, and Z are collinear and
\[\frac{YX}{ZX } = \frac{volume(upper)}{volume(lower) }\]
where volume(upper) and volume(lower) denote the volumes of the upper and lower trunks, respectively.
But X lies on HR, and Z and Y lie on FR and HS, respectively. Also, the lines HR, FQ, and IS are parallel to each other, as are the lines QS, FI, and ab, as well as the lines FR and HS. So ΔHYX is similar to ΔRZX and
\[\frac{Ia }{a S } = \frac{HX}{ XR} = \frac{ YX}{ ZX} = \frac{volume(upper) }{volume(lower)}\]
The final trick to determining the ratio between the trunk and the cylinder is to use Euclid V.18 (a.k.a. adding "one" to both sides of the above proportion) to arrive at
\[\eqalign{ \frac{IS}{a S} & = \frac{(Ia + a S}{a S } \cr &= \frac{Ia}{a S } + 1 \cr &= \frac{ volume(upper)}{ volume(lower)} + 1 \cr &= \frac{volume(upper) + volume(lower)}{ volume(lower)} \cr &= \frac{ cyl(AB)}{trunk(AB)}. \cr }\]
where cyl(AB) denotes the volume of the cylinder over AB and trunk(AB) denotes the volume of the lower trunk over AB as before. Now IS is the radius of rotation. Also, recall that a is the center of gravity of the original figure. Therefore, aS is the distance between the center of gravity of the original figure and the axis of rotation. So after taking reciprocals and multiplying numerator and denominator by 2π, we have proved the key ratio between the trunk and the cylinder: If AB is a 2-dimensional figure symmetric about an axis, then
\[\frac{ trunk(AB)}{cyl(AB) } = \frac{aS }{ IS} = \frac{2 \pi aS}{ 2 \pi IS} = \frac{ circum(a) }{ circum(AB) }\]
where circum(a) denotes the circumference of the circle with radius the distance between the center of gravity and the axis of rotation and circum(AB) denotes the circumference of the circle with radius equal to the radius of rotation.
Andrew Leahy (Knox College), "James Gregory and the Pappus-Guldin Theorem - A Ratio Between the Trunk and the Cylinder," Convergence (May 2019), DOI:10.4169/loci003262




