- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
James Gregory and the Pappus-Guldin Theorem - More on the Trunk and the Cylinder
If AB and EF are two planar figures with centers of gravity a and e, respectively, and which generate cylinders with the same height, we saw previously that
\[{ rev(AB) \over rev(EF)} = { trunk(AB) \over trunk(EF)} { circum(AB) \over circum(EF)}\]
Next, we multiply by one (in the very useful form something/something) twice and substitute in the ratio between the trunk and cylinder from the last section. This gives
\[\eqalign{ { rev(AB) \over rev(EF)} &= { trunk(AB) \over trunk(EF)} { circum(AB) \over circum(EF)} \cr &= { trunk(AB) \over cyl(AB)}{ cyl(AB) \over cyl(EF)} {cyl(EF) \over trunk(EF)} { circum(AB) \over circum(EF)} \cr &= {circum(a) \over circum(AB)} { cyl(AB) \over cyl(EF)} { circum(EF) \over circum(e)} { circum(AB) \over circum(EF)} \cr &= {circum(a) \over circum(e)}{ cyl(AB) \over cyl(EF)} \cr &= {circum(a) \over circum(e)} { area(AB) \over area(EF)} \cr }\]
where this last equation follows since the cylinders over AB and EF have the same height and hence the volumes are in the same ratios as the bases.
Notice that this is Pappus' version of the Pappus-Guldin theorem. The problem is that this proof only holds if both of the figures AB and EF are symmetric about an axis perpendicular to the axis of rotation. But it is not difficult to drop this requirement. If AB is not symmetric around such an axis, it can be reflected around an axis perpendicular to the axis of rotation to generate a figure HI consisting of two copies of AB which is symmetric around an axis.
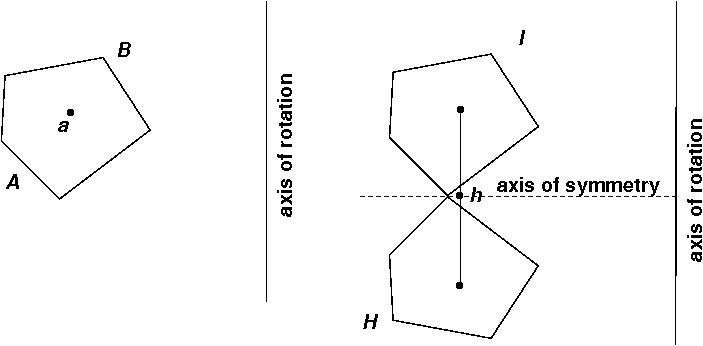
Archimedes' result shows that the center of gravity h of HI will be the midpoint of the segment connecting the centers of gravity of the two reflected copies of AB. Since the axis of reflection is perpendicular to the axis of rotation, the centers of gravity of the two reflected copies of AB will be the same distance from the axis of rotation and hence the line connecting them will be parallel to the axis of rotation. In other words, the center of gravity of HI will be the same distance from the axis as the center of gravity a of AB, or circum(a) = circum(h). Note also that area(HI) = 2 area(AB) and rev(HI) = 2 rev(AB) since HI is twice the size of AB. Similar arguments apply to a symmetric figure JK with center of gravity j constructed in the same way from EF. So the result for symmetric figures implies
\[{2 \,rev(AB) \over 2\, rev(EF)} = { rev(HI) \over rev(JK)} = {circum(h) \over circum(j)} {area(HI) \over area(JK)} = {circum(a) \over circum(e)}{ 2\, area(AB) \over 2\, area(EF) }\]
Cancel off the 2's and the restriction of having a figure symmetric about an axis is removed.
Andrew Leahy (Knox College), "James Gregory and the Pappus-Guldin Theorem - More on the Trunk and the Cylinder," Convergence (February 2010), DOI:10.4169/loci003262




