- About MAA
- Membership
- MAA Publications
- Periodicals
- Blogs
- MAA Book Series
- MAA Press (an imprint of the AMS)
- MAA Notes
- MAA Reviews
- Mathematical Communication
- Information for Libraries
- Author Resources
- Advertise with MAA
- Meetings
- Competitions
- Programs
- Communities
- MAA Sections
- SIGMAA
- MAA Connect
- Students
- MAA Awards
- Awards Booklets
- Writing Awards
- Teaching Awards
- Service Awards
- Research Awards
- Lecture Awards
- Putnam Competition Individual and Team Winners
- D. E. Shaw Group AMC 8 Awards & Certificates
- Maryam Mirzakhani AMC 10 A Awards & Certificates
- Two Sigma AMC 10 B Awards & Certificates
- Jane Street AMC 12 A Awards & Certificates
- Akamai AMC 12 B Awards & Certificates
- High School Teachers
- News
You are here
Mathematical Treasures - Frans van Schooten's Exercitationes mathematicae

This is the title page of Exercitationes mathematicae libri quinque (Five Books of Mathematical Exercises) (1657) by Frans van Schooten (1615–1660). In particular, according to the inscription, this copy was originally owned by Johann Hudde (1628–1704), a student of van Schooten. The five books collected in this work contained a variety of mathematical material, including sections on basic arithmetic and geometry, simple geometric constructions, an attempted reconstruction of a work of Apollonius, constructions of conic sections, and some combinatorial techniques enabling him to find amicable numbers. Van Schooten also included as an appendix the first text on probability, written by Christiaan Huygens (1629–1695), again one of his students. This collection was one of the books read by Isaac Newton while he was a student at Cambridge University and helped to introduce him to modern mathematics.

This is page 167 in the section on geometrical constructions. This particular construction shows how to find the distance across a river.

On p. 223, van Schooten begins his section on reconstruction of the Plane Loci of Apollonius. Interestingly, although van Schooten only knew of the Plane Loci from various Greek references, more recently the actual work was discovered in an Arabic version.

On p. 224, van Schooten shows how, given points A and B, to construct two line segments AG and BG that meet at a given angle.
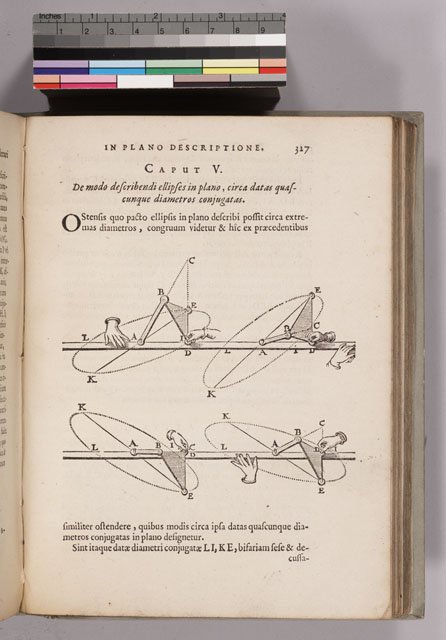
On page 327, van Schooten demonstrates the use of linkages to construct ellipses.

On p. 533 is the final proposition in Huygens' Treatise on Reckoning in Games of Chance. This particular problem asks to determine the ratio of "chances" in a game where two people play alternately with two dice, on the condition that the first one wins when he throws a 7, while the second one wins if he throws a 6, assuming that the second player throws first. Huygens' solution is that the ratio is 31:30.

At the bottom of p. 533 and on p. 534 are five exercises that conclude Huygens' treatise. For example, in problem 2, Huygens sets up the situation where there are 12 balls in an urn, of which 4 are white and 8 are black. There are three blindfolded players A, B, and C who draw a ball out in turn with the winner being the first one to draw out a white ball. Huygens asks the ratio of the chances of the three players. (As stated, the problem is somewhat ambiguous, but it is probably easiest to assume that if a black ball is drawn, it is put back into the urn.)
Frank J. Swetz and Victor J. Katz, "Mathematical Treasures - Frans van Schooten's Exercitationes mathematicae," Convergence (January 2011)




